Формула 1.4.128
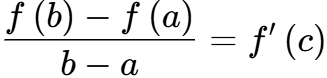
Формула Лагранжа
·
Просм.: 38
·
Сохранений: 0
·
Ком.: 0
Пусть функция $$ f\left(x\right) $$ неприрывна на $$ a\le x\le b $$ и дифференцируема на $$ a . Тогда существует точка $$ c\in\left(a;b\right) $$ такая, что производная функции в ней равна угловому коэффициенту прямой, проведённой через точки $$ \left(a;f\left(a\right)\right) $$ и $$ \left(b;f\left(b\right)\right) $$